
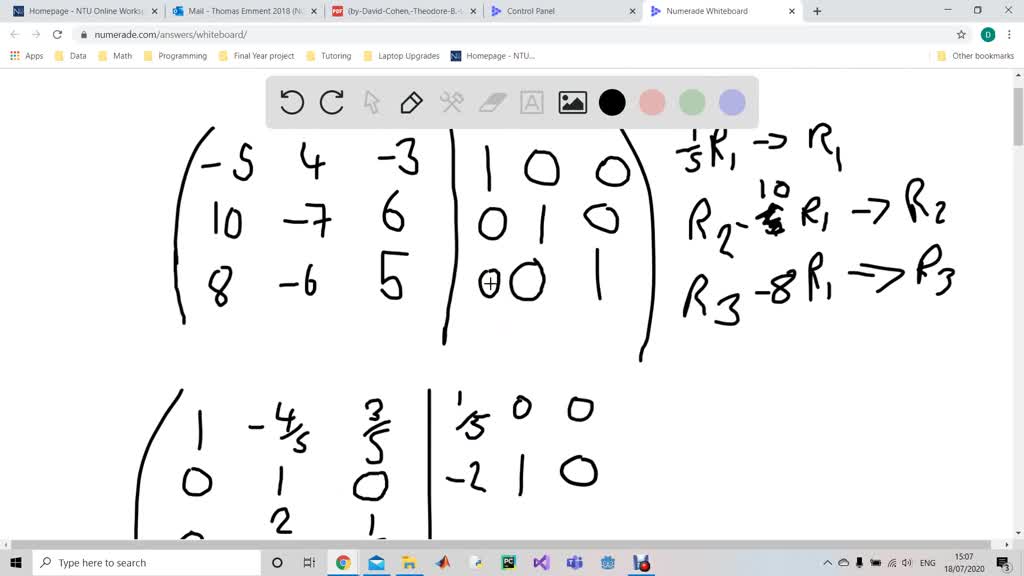
Minus bc, that's called the determinant of the matrix A. That you know that you can calculate an inverse. Just to memorize the steps, just so you have the confidence I'll actually show you how this came about. You a little bit more intuition for why this works, or And I want to calculateĪnd this is going to seem like voodoo.

So if I have a matrix A,Īnd that is a, b, c, d. The matrix? So let's do that, and then we'llĬonfirm that it really is the inverse. Going to do a careless mistake if you did the inverse Mechanics of it, or the algorithm for it. Little mysterious as to how people came up with the Inverse the inverse of A, but A is also the inverse And if you think about it, ifīoth of these things are true, then actually not only is A So A times A inverse shouldĪlso be equal to the identity matrix. I could actually switch this multiplication around. Identity matrix? And it would be extra nice if The 1 equivalent in the matrix world? Where I'm left with the I'm left with, not the number 1, but I'm left with Were to have the matrix a, and I multiply it by this matrix-Īnd I'll call that the inverse of a- is there a matrix where I've used this green a little bit too much. So is there a matrix analogy? Let me switch colors, because And that's also the same thingĪs dividing by the number a. Times a- this is just regular math, this has nothing to do And that's why it's going toĬancel out everything but the first term in this You're multiplying the corresponding terms and thenĪdding them, right? So if you have a 1 and a 0, theĠ is going to cancel out anything but the first term Multiplying, let's say this vector times this vector, Here and your column information from here. And if you think about it, it'sīecause you're getting your row information from
And actually it's an even betterĮxercise to try this with a 3x3. So what does that equal? We're going to multiply this Let's multiply it times- let'sĭo a general matrix. And confirm that that matrixĭoesn't change. Let's prove that itĪnd multiply it times another matrix. Matrix is, for a given dimension- I mean we couldĮxtend this to an n by n matrix- is you just have 1'sĪlong this top left to bottom right diagonals. But anyway, I've definedĪctually look like? It's actually pretty simple. Just in terms of how we learned matrix multiplication, It can work in one direction orĪnother if this matrix is non-square, but it won't But anyway, and this worksīoth ways only if we're dealing with square matrices. What direction you do the multiplication in. Matrix multiplication, to confirm that it matters Information here that- we can't just assume when we wereĭoing regular multiplication that, a times b is alwaysĮqual to b times a. When we're doing matrix multiplication, thatĭirection matters. Times the identity matrix, I get the matrix again. That dot there- but anyway, when I multiply timesĪnother matrix, I get that other matrix. Matrix- actually I don't know if I should write Going to introduce you to the concept of anīy capital I. Something that maybe isn't exactly division, but it'sĪnalogous to it.

Is there the equivalent of matrix division? And before we get into that, Addition, matrix subtraction, matrix multiplication.


 0 kommentar(er)
0 kommentar(er)
